30  Lojistik Regresyon

Bu çalışmada, programda mevcut olan Smarket veri seti (Borsa ile alakalı veriler bulunmaktadır.) üzerinden lojistik regresyon testi gerçekleştirilmiştir. Mevcut borsa verileri kullanılarak model oluşturulup tahminler yapılacaktır ve bu tahminlerin güvenilirliği test edilecektir.

Öncelikle veri setinin olduğu kütüphaneyi çağıralım:

Smarket veri setini inceleyelim ve veri setini daha rahat çalışabilmek adına attach fonksiyonu ile R çevresine bağlayalım:

colnames(Smarket)
[1] "Year"      "Lag1"      "Lag2"      "Lag3"      "Lag4"      "Lag5"     
[7] "Volume"    "Today"     "Direction"
dim(Smarket)
[1] 1250    9
summary(Smarket)
      Year           Lag1                Lag2                Lag3          
 Min.   :2001   Min.   :-4.922000   Min.   :-4.922000   Min.   :-4.922000  
 1st Qu.:2002   1st Qu.:-0.639500   1st Qu.:-0.639500   1st Qu.:-0.640000  
 Median :2003   Median : 0.039000   Median : 0.039000   Median : 0.038500  
 Mean   :2003   Mean   : 0.003834   Mean   : 0.003919   Mean   : 0.001716  
 3rd Qu.:2004   3rd Qu.: 0.596750   3rd Qu.: 0.596750   3rd Qu.: 0.596750  
 Max.   :2005   Max.   : 5.733000   Max.   : 5.733000   Max.   : 5.733000  
      Lag4                Lag5              Volume           Today          
 Min.   :-4.922000   Min.   :-4.92200   Min.   :0.3561   Min.   :-4.922000  
 1st Qu.:-0.640000   1st Qu.:-0.64000   1st Qu.:1.2574   1st Qu.:-0.639500  
 Median : 0.038500   Median : 0.03850   Median :1.4229   Median : 0.038500  
 Mean   : 0.001636   Mean   : 0.00561   Mean   :1.4783   Mean   : 0.003138  
 3rd Qu.: 0.596750   3rd Qu.: 0.59700   3rd Qu.:1.6417   3rd Qu.: 0.596750  
 Max.   : 5.733000   Max.   : 5.73300   Max.   :3.1525   Max.   : 5.733000  
 Direction 
 Down:602  
 Up  :648  
           
           
           
           
attach(Smarket)

Burada attach fonksiyonu ile verimizi R çevresine bağlayabiliyoruz. Bu sayede veri çerçevesi içindeki sütun isimlerine doğrudan erişebiliriz.

Bu modelleme çalışmasındaki amacımız borsanın o günkü seyrini (Direction değişkeni), son beş gün boyunca borsa kapanışı ve o günkü alış satış hacmini kullanarak tahmin etmeye çalışıyoruz.

Verilerle bir model oluşturalım. modeli setteki Directionc verisine göre kurup modelin özetini inceleyelim; modele, modeli tanımlayacak bir isim atayarak glm fonksiyonu ile oluşturduk.

glm.fits <- glm(data = Smarket, Direction~Lag1 + Lag2 +Lag3+ Lag4+ Lag5+ Volume, family = binomial)
summary(glm.fits)

Call:
glm(formula = Direction ~ Lag1 + Lag2 + Lag3 + Lag4 + Lag5 + 
    Volume, family = binomial, data = Smarket)

Coefficients:
             Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.126000   0.240736  -0.523    0.601
Lag1        -0.073074   0.050167  -1.457    0.145
Lag2        -0.042301   0.050086  -0.845    0.398
Lag3         0.011085   0.049939   0.222    0.824
Lag4         0.009359   0.049974   0.187    0.851
Lag5         0.010313   0.049511   0.208    0.835
Volume       0.135441   0.158360   0.855    0.392

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 1731.2  on 1249  degrees of freedom
Residual deviance: 1727.6  on 1243  degrees of freedom
AIC: 1741.6

Number of Fisher Scoring iterations: 3

Predict fonksiyonu ile modelimizin ilk 10 parametresini tahmin edelim:

predict.glm(glm.fits, type = "response")[1:10]
        1         2         3         4         5         6         7         8 
0.5070841 0.4814679 0.4811388 0.5152224 0.5107812 0.5069565 0.4926509 0.5092292 
        9        10 
0.5176135 0.4888378

Tahminleri yeni bir veri içine aktaralım, bu şekilde yeni verimizle sadece tahmin üzerinden işlem yapabiliriz.

Öncelikle tahmin ettiğimiz Direction verilerinin olasılık değerlerini alalım:

glm_prob <- predict.glm(glm.fits, type = "response")

Yeni oluşturduğumuz tahmin veri setinin ilk 6 elemanını inceleyelim:

head(glm_prob)
        1         2         3         4         5         6 
0.5070841 0.4814679 0.4811388 0.5152224 0.5107812 0.5069565

Ve tahmin veri setimizin histogramını oluşturduktan sonra tahmin veri seti için olasılık veri seti oluşturalım:

hist(glm_prob)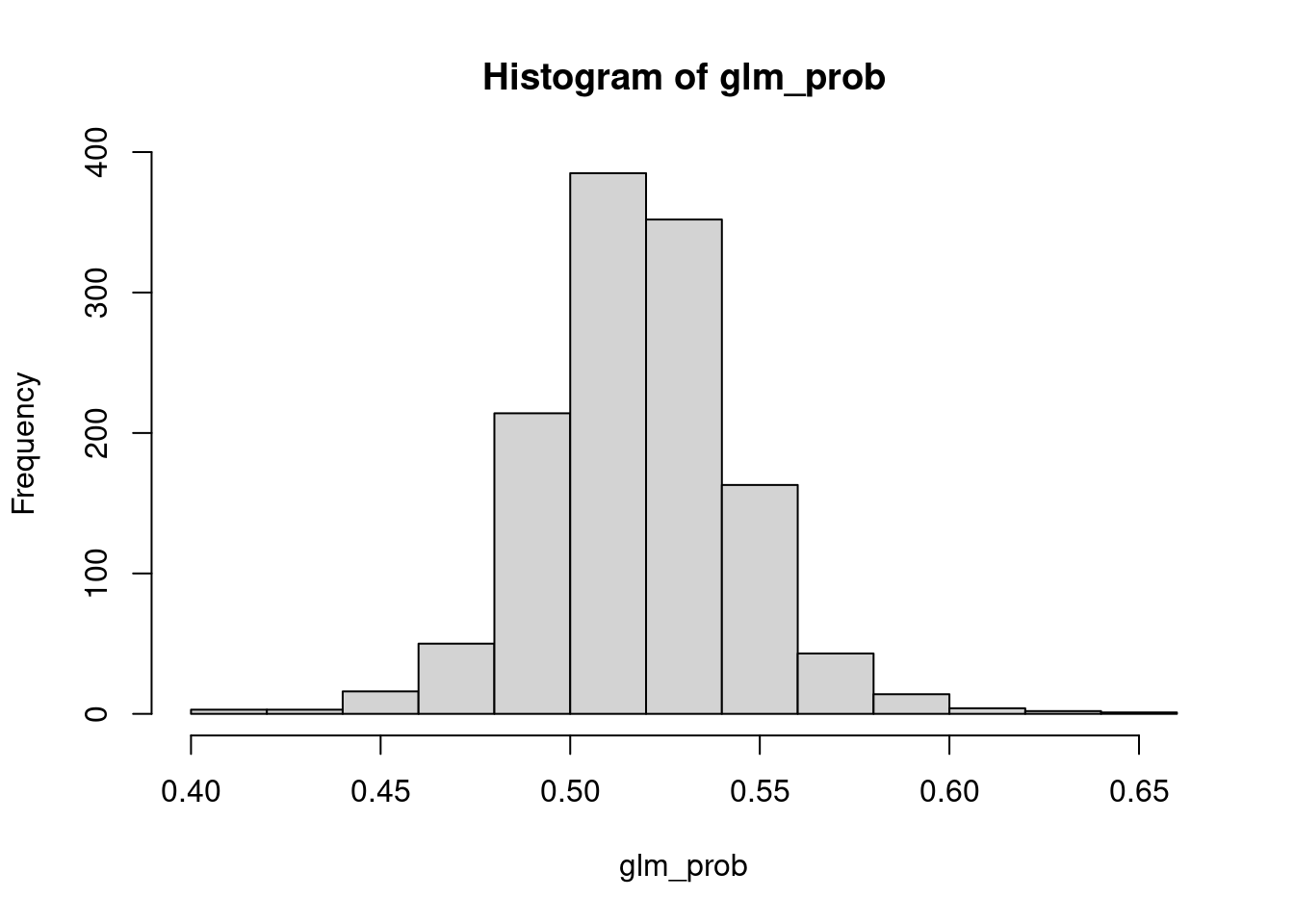

Sadece histograma baktığımızda tahmin verilerimizin bir bölgede gruplandığını görebiliriz. Bu bölgeyi sınır noktası olarak kabul ederek çalışmayı 1-0 moduna indirgeyebiliriz. Bu şekilde pozitif ve negatif sonuçlar alabiliriz.

sum fonksiyonu ile 0.5 olarak kabul ettiğimiz ayrımın altında ve üstünde kalan değerlerin sayısını inceleyelim. Bunların hepsi toplandığında dim fonksiyonu ile incelediğimiz veri seti boyutunu elde etmemiz gerekir.

Kaç tane tahmin olaslığı 0.5’den büyük?

sum(glm_prob > 0.5)
[1] 964

Kaç tanesi 0.5’den küçük?

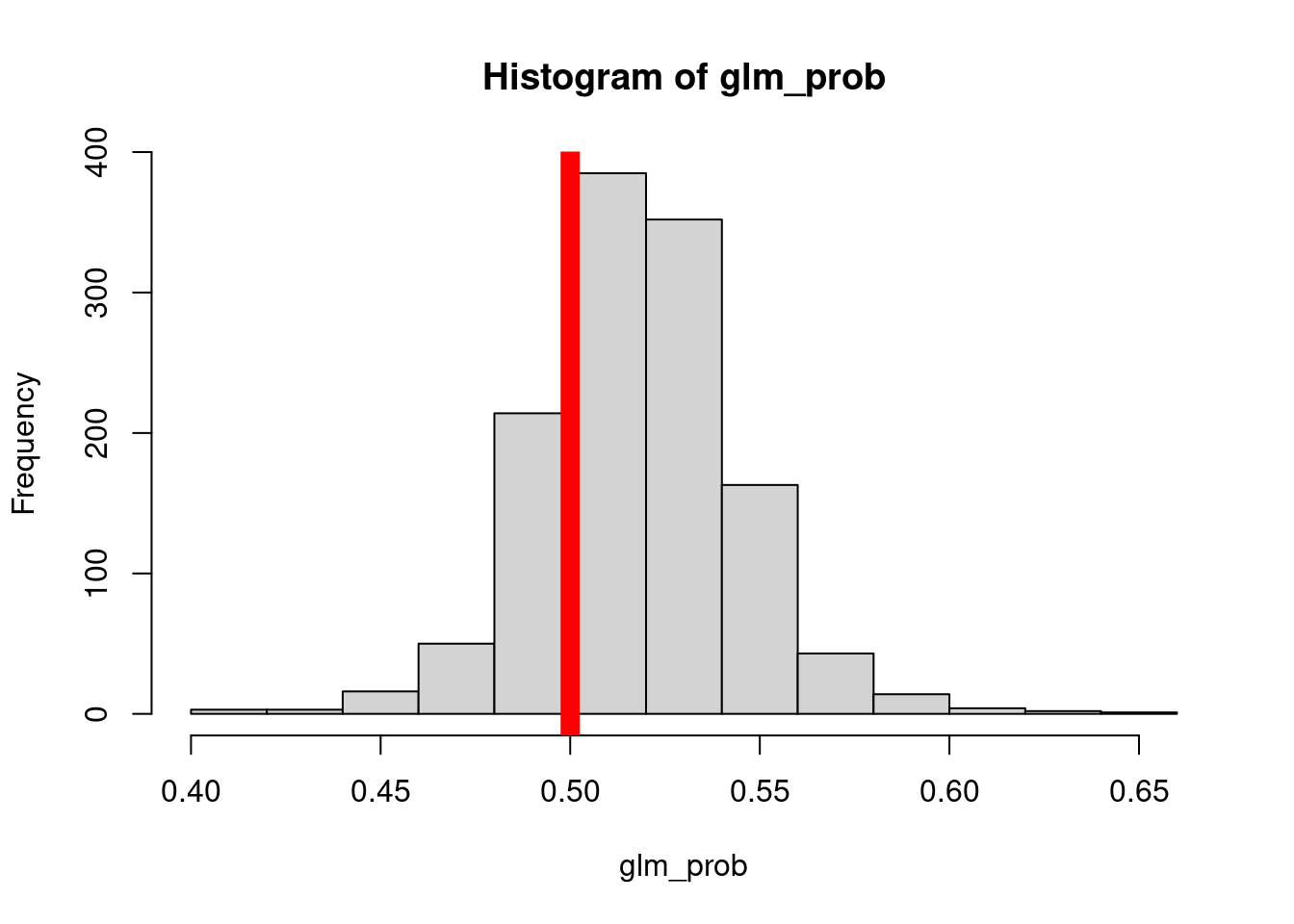
sum(glm_prob < 0.5)
[1] 286

Şimdi aynı histogramın 0.5 değerini çizgi ile gösteren versiyonunu oluşturalım:

hist(glm_prob)

abline(v=0.5, col="red", lwd=10)

Şimdi bu değerleri Aşağı (Down) ve Yukarı (Up) olarak tanımlayalım.

glm_pred<- rep("Down", 1250)

glm_pred[glm_prob> 0.5]  <- "up"

Şimdi bu tanımlanan değerlerin table fonksiyonu ile frekans tablosunu oluşturup sağlamasını yapalım:

table(glm_pred)
glm_pred
Down   up 
 286  964

Veri seti içindeki herhangi bir verinin aşağı ve yukarı olarak nasıl gösterilebileceğine bakalım, burada Direction verisinin ilk 5 satırı incelenmiştir. Down olarak gösterilenler 0.5’ten küçük, up olarak gösterilenler ise 0.5’ten büyük olan değerlerdir.

Peki, gerçek değerlerimiz nedir?

Smarket$Direction[1:5]
[1] Up   Up   Down Up   Up  
Levels: Down Up

Şimdi ise, hem gerçek hem de tahmin edilmiş değerlerden bir karmaşa matrisi oluşturalım:

table(Smarket$Direction, glm_pred)
      glm_pred
       Down  up
  Down  145 457
  Up    141 507

Karmaşa matrisi, bir modelin performansını ölçmek için kullanabikeceğiniz bir frekans tablosu olarak tanımlanabilir.

Az önceki tabloyu oluşturmak için; gerçek değerleri, tahmin edilen değerlerle karşılaştırdık. Basit olsun diye, 1 ve 0 olarak iki durumumuz olsun.

Toplam örneklem sayımız ise: \(N = TP + TN + TN + FP\)

Bu değerlerin hepsini aşağıdaki şekilde özetleyebiliriz:

knitr::include_graphics(path = "../images/conf_tbl.png")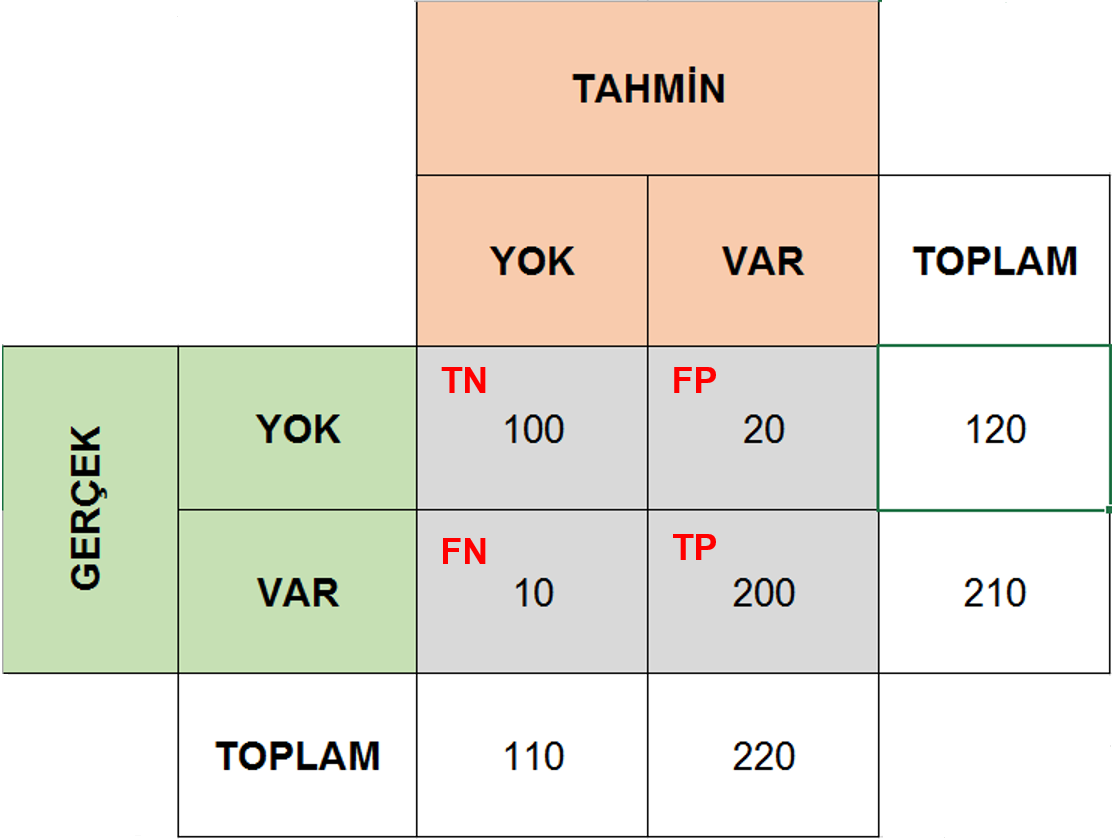

Bu veri setinde borsa değerleri vardı ve borsadaki düşüşleri ve yükselişleri temsil etmek adına ölçümlerimizi up ve down olarak tanımladık.

Pozitif ve negatiften (1-0) bahsetmiştik. Karmaşa matriksinde bu değerlerin temsil ettiği durumlar şu şekildedir:

Bir takım basit matematiksel formüllerle bu değer oranlarına bakılarak veri seti üzerinde oluşturulan modellerin güvenilirliği incelenebilir.

\[ Doğruluk (Accuracy) = \frac{TP + TN}{N} \] Doğruları ve yanlışları ne kadar yüksek oranda belirleyebilirsek, modelimizin doğruluk payı o kadar yüksektir.

\[ Hata Oranı (Error Rate) = \frac{FN + FP}{N} \]

\[ Hata Oranı (Error Rate) = 1 - Doğruluk (Accuracy) \] Elimizdeki gerçek değerlerin ne kadarını doğru tahmin etmişiz?

\[ DoğruPozitifOranı = \frac{TP}{FN + TP} \]

Elimizdeki gerçek değerlerin ne kadarını yanlış tahmin etmişiz?

\[ Yanlış Pozitif Oranı = \frac{FP}{TN + FP} \]

Peki yaptığımız tahminlerin ne kadarı doğru?

\[ Hassasiyet (Precision) = \frac{TP}{TP + FP} \]

Peki bu öğrendiklerimizi neye ölçekleyebiliriz?

Yeni bir hastalık tanı kiti oluşturduğumuzu düşünelim ve bu kitin performansını test etmek istiyoruz.

Sizce ne yapabiliriz? İlk olarak hasta ve sağlıklı olduklarından emin olduğumuz bir grup kişi ile çalışmaya başlayabiliriz. Sonra bu kişilerden alınan örnekleri geliştirdiğimiz kit ile test ederek bir tahmin elde edebiliriz.

Elde edeceğimiz sonuç ya hasta ya da sağlıklı olacaktır.

Amacımız sizce ne olabilir? Mantık olarak; gerçekten hasta olan kişileri hasta olarak, gerçekten sağlıklı olan kişileri de sağlıklı olarak tahmin edebiliyorsak kitimiz doğru çalışıyor demektir. Modelmizin ya da test kitimizin Doğruluk değer ne kadar yüksekse o kadar iyi çalışan bir kitimiz var demektir.