install.packages("ISLR2")19 Doğrusal modelleme
19.1 Kütüphanler
Bu kısım kapsamında kullanılacak veri setlerinin ve fonksiyonlar için iki farklı kütüphane gereklidir:
-
MASS(R içerisinde gelmektedir.) -
ISLR2(Bu kütüphanenin yüklenmesi gerekidir.)
Eğer daha önce ISLR2 paketini yüklemediyseniz öncelikle aşağıdaki gibi bu paketi yüklemelisiniz:
Daha sonra bu paketleri çalışma ortamımıza yükleyelim:
19.2 Basit doğrusal regresyon
Bu uygulama kapsamında ISLR2 paketi içerisindeki Boston veri setini kullancağız. Öncelikle veri setinin ilk beş satırını inceleyelim:
head(Boston) crim zn indus chas nox rm age dis rad tax ptratio lstat medv
1 0.00632 18 2.31 0 0.538 6.575 65.2 4.0900 1 296 15.3 4.98 24.0
2 0.02731 0 7.07 0 0.469 6.421 78.9 4.9671 2 242 17.8 9.14 21.6
3 0.02729 0 7.07 0 0.469 7.185 61.1 4.9671 2 242 17.8 4.03 34.7
4 0.03237 0 2.18 0 0.458 6.998 45.8 6.0622 3 222 18.7 2.94 33.4
5 0.06905 0 2.18 0 0.458 7.147 54.2 6.0622 3 222 18.7 5.33 36.2
6 0.02985 0 2.18 0 0.458 6.430 58.7 6.0622 3 222 18.7 5.21 28.7Bu veri seti Boston’un 506 farklı bölgesindeki evlerin fiyatlarını göstermektedir. Şimdi kullanacağımız sütun isimlerine bakalım:
-
medv: ortanca ev fiyatı, her bölgedeki ortanca ev fiyatını belirtmektedir. -
lstat: her bölgede bulunan sosyoekonomik açıdan düşük gelir seviyesine sahip ev sayısı.
Bu veri seti hakkında daha fazla bilgi almak için bu bağlantıya tıklayınız.
Bu çalışma kapsamında medv ve lstat değişkenleri arasındaki ilişkiyi doğrusal regresyon ile modellemeye çalışacağız. Acaba bir mahallenin sosyoekonomik statüsü, mahalledeki evlerin fiyatını etkiliyor mu?
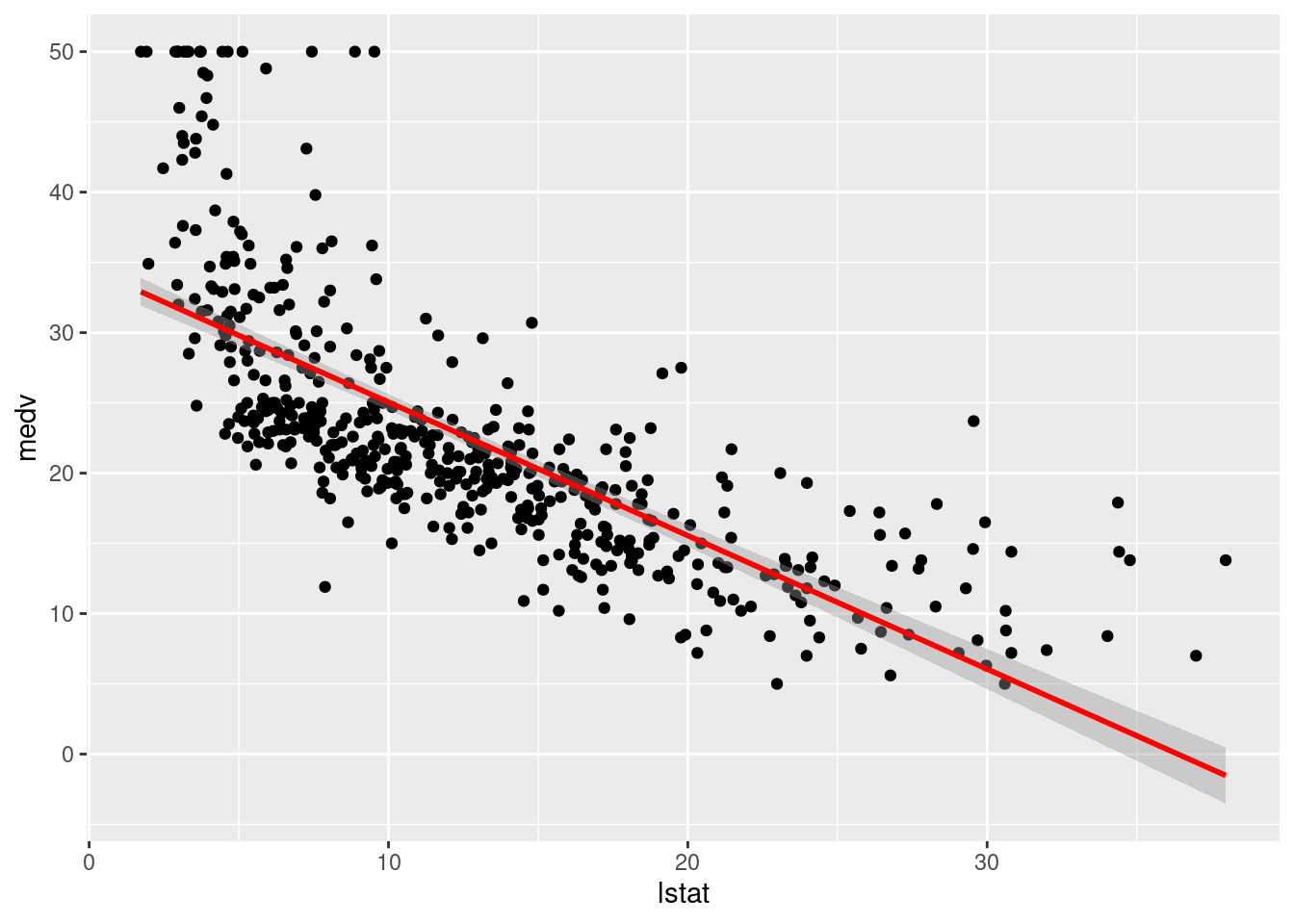
Öncelikle bu iki değişken arasındaki ilişkiyi görselleştirelim. Bunun için basitçe bir grafik kullanabiliriz (Şekil @ref(fig:bostonplot)):
plot(medv~lstat, data = Boston)
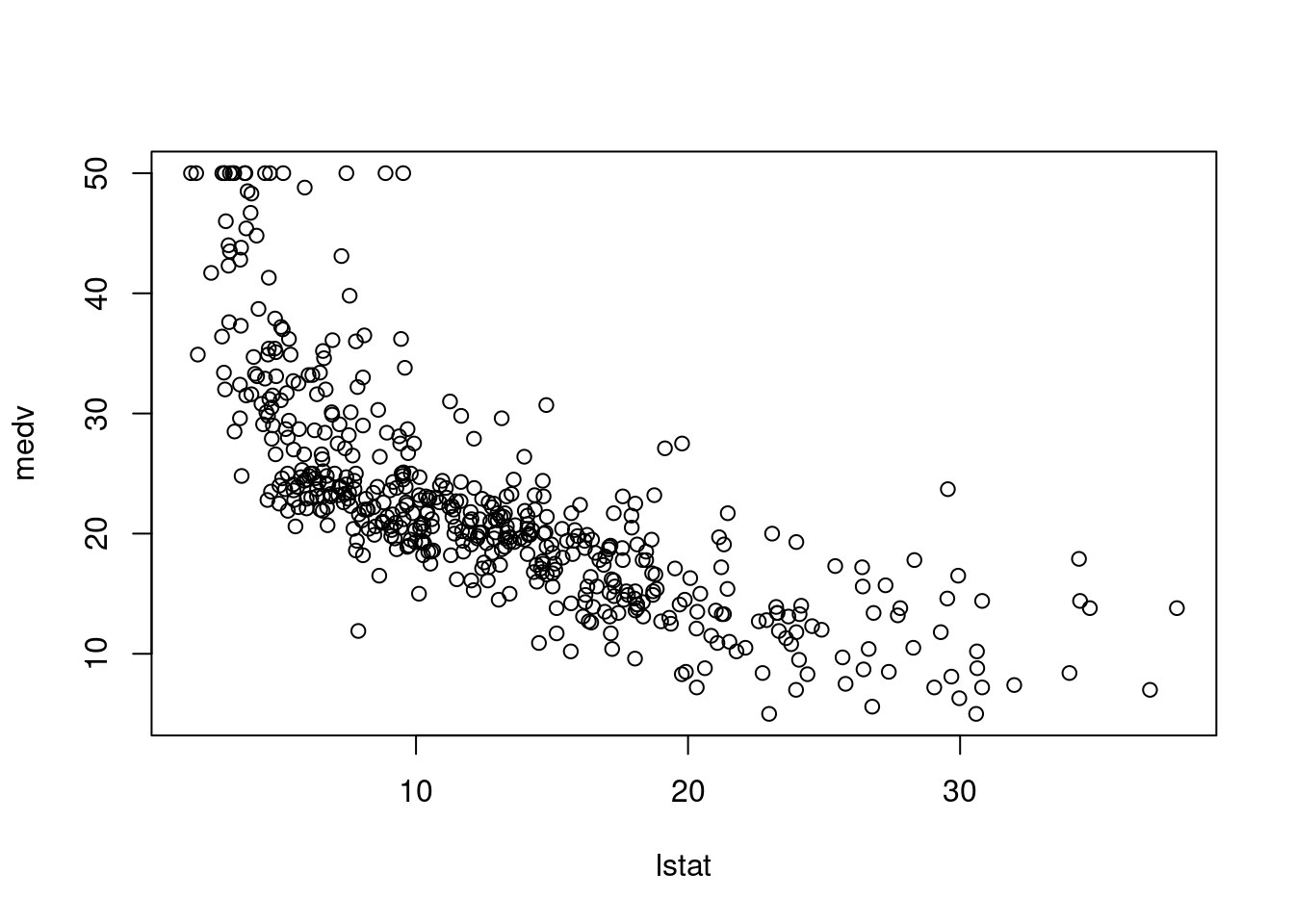
medv ve lstat değişkenleri arasındaki ilişkiR üzerinde herşeyin birden çok çözüm yolu bulunmaktadır. Mesela bu grafiği oluşturmak için üç farklı yol kullanabiliriz:
Burada kullandığımız attach foknsiyonu, bahsi geçen veri setinde bulunan sütunları doğrudan kullanmamızı sağlar. Dolayısıyla, veri setini bir kere attach foksiyonu ile bağladık mı sütun isimlerini doğrudan kullabiliriz.
Ancak kodlarımızın daha açık ve okunabilir olması açısından ben aşağıdaki tarzı tercih edeceğim:
plot(medv~lstat, data = Boston)Sizce bu şekil ne anlatıyor? Sosyoekonomik seviye düşüşü ev fiyatlarını sizce nasıl etkiliyor olabilir? Bu noktada bir durup düşünün.
Peki bu iki değişken arasındaki ilişkiyi doğrusal regresyon ile nasıl modelleyebilriz?
lm.fit <- lm(medv ~ lstat, data = Boston)Modelin sahip olduğu bilgileri almak için summary fonksiyonunu kullanabiliriz. Bu sayede \(p\)-değerlerini inceleyebiliriz:
summary(lm.fit)
Call:
lm(formula = medv ~ lstat, data = Boston)
Residuals:
Min 1Q Median 3Q Max
-15.168 -3.990 -1.318 2.034 24.500
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 34.55384 0.56263 61.41 <2e-16 ***
lstat -0.95005 0.03873 -24.53 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 6.216 on 504 degrees of freedom
Multiple R-squared: 0.5441, Adjusted R-squared: 0.5432
F-statistic: 601.6 on 1 and 504 DF, p-value: < 2.2e-16Modeldeki isimleri elde etmek için;
names(lm.fit) [1] "coefficients" "residuals" "effects" "rank"
[5] "fitted.values" "assign" "qr" "df.residual"
[9] "xlevels" "call" "terms" "model" Modeldeki katsayıları elde etmek için coef fonksiyonunu kullabiliriz:
coef(lm.fit)(Intercept) lstat
34.5538409 -0.9500494 Elde ettiğimiz katsayılar aslında derslerde gördüğümüz \(\beta_{0}\) ve \(\beta_{1}\) parametrelerini ifade etmektedir.
Güven aralıklarını (%95) elde etmek için ise confint fonkisyonunu kullanabiliriz:
confint(lm.fit) 2.5 % 97.5 %
(Intercept) 33.448457 35.6592247
lstat -1.026148 -0.8739505Güven aralıkları kısmı tekrar yazılacaktır!
Eğer Şekil @ref(fig:bostonplot)’i dikkatle incelerseniz, iki değişken arasında doğrusal olmayan bir ilişki görebilme imkanınız var. Derslerde de belirttiğimiz gibi aslında mükemmel bir doğrusal ilişki bulma imkanınız yok. Bizim burada yaptığımız ise, aslında iki değişken arasındaki ilişkiyi en iyi ifade eden doğrusal modeli elde etmek.
Bunu daha iyi olarak doğrusal modeli çizerek gösterebiliriz (Şekil @ref(fig:lm)).
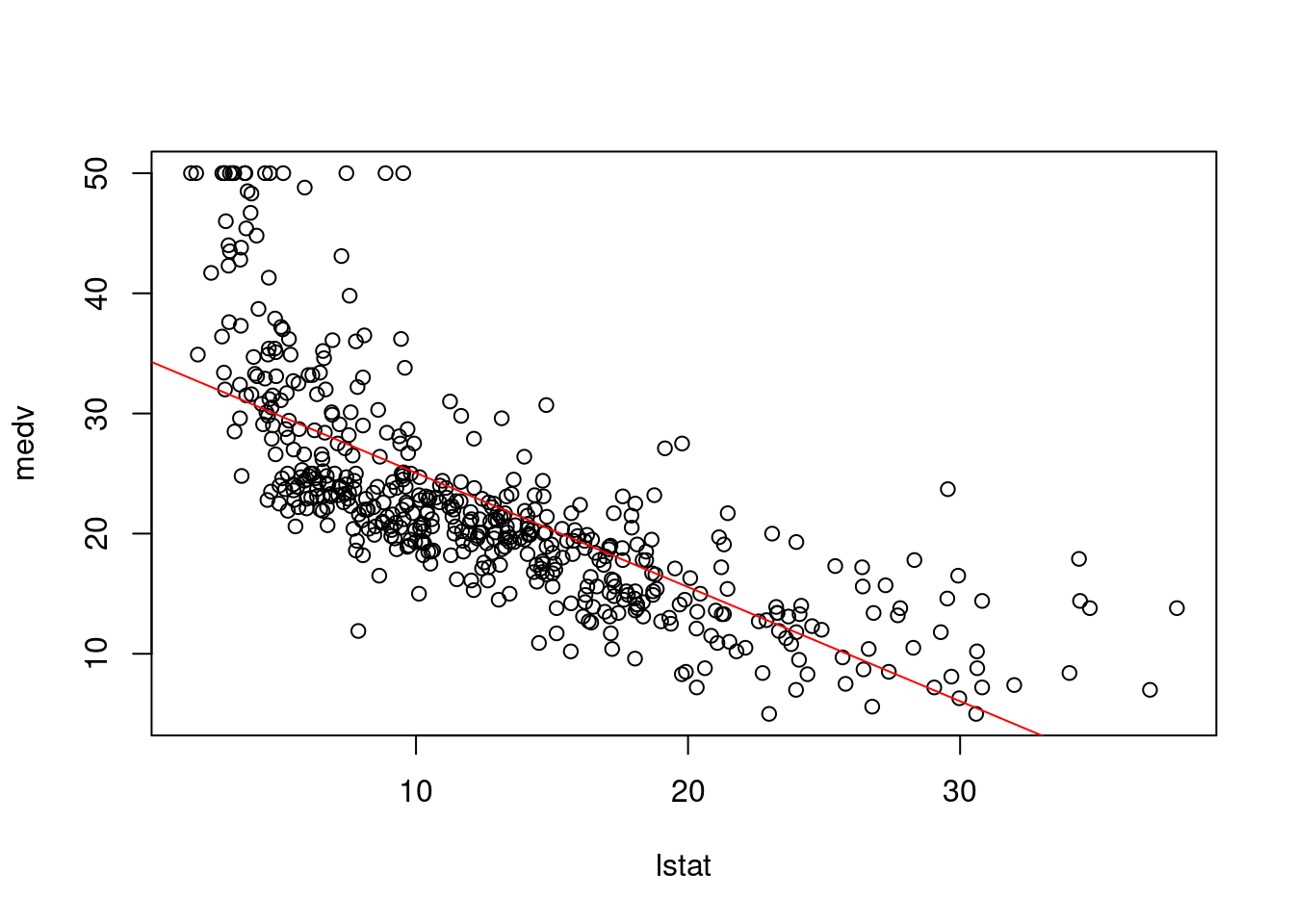
Son olarak R bize farklı grafikler ile oluşturduğumuz model hakkında daha fazla bilgi vermektedir (Şekil @ref(fig:diagnostic)). Burada dikkat etmemiz gereken grafik sol üstteki Residuals cs Fitted grafiği. Derste, artıklardan bahsetmiştik. Bu artık değerlerinin homojen bir şekilde doğrusal modelin etrafında dağıması ideal olacaktır. Aslında x eksenindeki girdi ile, artıklar arasında hiç bir ilişkinin olmaması gerekir.
opar <- par(no.readonly = TRUE) # copy of current settings
par(mfrow = c(2, 2)) # 2 * 2
plot(lm.fit)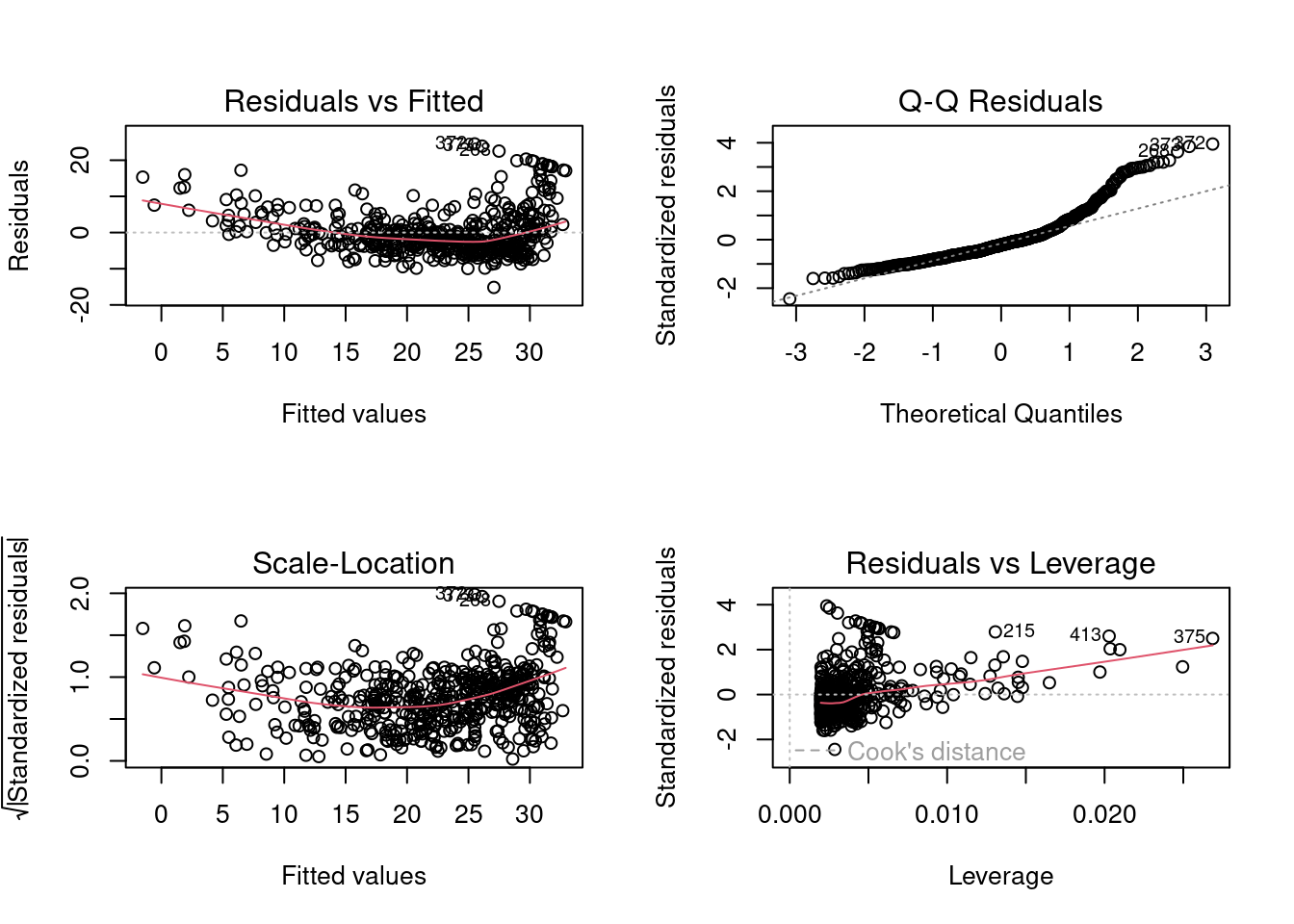
İdeal olarak baktığımızda artık değerlerinin aslında çizdiğimiz doğrusal model etrafında homojen bir şekilde dağılmasını bekleriz. Bu bize aslında artık değerleriyle \(x\) eksenindeki değişken arasında bir ilişki olmamasını beraberinde getirir.
Ancak grafiğe baktığımızda artıklar ile x arasında az da olsa bir ilişki var. Bu çok istenen bir durum değildir. Benim bu noktadaki yorumum şu olur:
Elimizdeki değişkenler arasında doğrusal bir ilişki olmadığı için artıklar doğrusal model etrafında homojen bir şekilde dağılmamıştır.
19.3 Ekstralar: ggplot ile denemeler
Eğer buraya kadar geldiyseniz ggplot2’yi mutlaka denemelisiniz. Şimdi aynı grafikleri ggplot2 ile tekrarlayalım (Şekil @ref(fig:try)). R üzerinde harka görselleştirme araçları mevcuttur. Bununla ilgili görselleştirmeleri internet sitesinde paylaştım.
library(ggplot2)
ggplot(data = Boston, aes(x = lstat, y = medv)) +
geom_point() +
geom_smooth(method = "lm", color = "red")`geom_smooth()` using formula = 'y ~ x'