15 Bilimsel Hikaye Anlatımı 1

Bu noktaya kadar R üzerinde veri tiplerini, vektörleri, listeler ve veri çerçevelerini öğrendik. Hatta bilgisayardaki verileri okuduk. Bu sayede basit vektörel işlemler yaptık. Mesela boyu belirli bir değerden büyük olan kişileri seçtik. Ya da boy ve kilo değişkenlerini kullanarak vücut kütle endeksi bile hesapladık. Peki bundan sonra ne olacak?

Veri analizi aslında bilimsel bir hikaye anlatıcılığıdır. Nasıl bir hikaye anlatıcısı üslubuyla, benzetmeleriyle, kelime oyunlarıyla bize bir öykü anlatıyorsa; biz de tablolarımızla, grafiklerimizle ve istatsisitk bilgimizle okuyuculara bilimsel bir öykü anlatıyoruz. Bu öykü anlatıcılığındaki ilk adım ise elimizdeki verinin ne olduğunu tanımlamak. İşte bunu tanımlayıcı istatistik olarak isimlendiriyoruz.

Öncelikle R üzerinde gelen öntanımlı iris veri setini kullanarak işe başlayalım.

Bu veri çerçevesinin sütun isimlerini elde edelim:

colnames(iris)

[1] "Sepal.Length" "Sepal.Width"  "Petal.Length" "Petal.Width"  "Species"

Bu veri seti, iris biktisinin üç farklı türüne ait sepal uzunluğu, sepal genişliği, petal uzunluğu, petal genişliği ve tür isimleri gibi farklı değişkenleri barındıryor.

Bu adımdan sonra kullanacağımız ilk fonksiyon summary olacak. Bir dosya okuduktan sonra her zaman bu fonksiyonla elde ettiğiniz veri çerçevesini özetlemenizi tavsiye ederim. Bu sayede elinizdeki verinin içeriğini öğrenmiş olacaksınız:

summary(iris)

  Sepal.Length    Sepal.Width     Petal.Length    Petal.Width   
 Min.   :4.300   Min.   :2.000   Min.   :1.000   Min.   :0.100  
 1st Qu.:5.100   1st Qu.:2.800   1st Qu.:1.600   1st Qu.:0.300  
 Median :5.800   Median :3.000   Median :4.350   Median :1.300  
 Mean   :5.843   Mean   :3.057   Mean   :3.758   Mean   :1.199  
 3rd Qu.:6.400   3rd Qu.:3.300   3rd Qu.:5.100   3rd Qu.:1.800  
 Max.   :7.900   Max.   :4.400   Max.   :6.900   Max.   :2.500  
       Species  
 setosa    :50  
 versicolor:50  
 virginica :50

Bu komut sonucunda, her sütuna ait farklı istatistik bilgiler elde ettik.

Peki bundan sonra ne olacak? Bu verilerle ne yapabiliriz?

Kaç tane var?
Neredeler?
Dağılımları nasıl? (homojen veya heterojen)

Sıra sıra gidelim…

15.1 Tanımlayıcı istatistikler

Tanımlayıcı istatistikler, genel olarak bir verideye üstten bir bakış atmamızı sağlar. Aslında bu veri içerisindeki ilişkileri, çıkarımsal olmayan bir şekilde görselleştirmeyi hedefliyoruz.

Veri çerçevesinde kaç eleman var?

dim(iris)

[1] 150   5

nrow(iris)

[1] 150

ncol(iris)

[1] 5

Ya da vektörlerin boyutlarını hesaplayabiliriz:

length(iris$Sepal.Length)

[1] 150

15.1.1 Frekans tabloları

Mesela bu veri çerçevesindeki tür isimleri için frekans tablosu oluşturalım. Bunun için table fonksiyonunu kullanacağız:

table(iris$Species)


    setosa versicolor  virginica 
        50         50         50

Peki şimdi rakam vektörlerinde kullanalım:

table(iris$Sepal.Length)


4.3 4.4 4.5 4.6 4.7 4.8 4.9   5 5.1 5.2 5.3 5.4 5.5 5.6 5.7 5.8 5.9   6 6.1 6.2 
  1   3   1   4   2   5   6  10   9   4   1   6   7   6   8   7   3   6   6   4 
6.3 6.4 6.5 6.6 6.7 6.8 6.9   7 7.1 7.2 7.3 7.4 7.6 7.7 7.9 
  9   7   5   2   8   3   4   1   1   3   1   1   1   4   1

Sanırım bu fonkisyon rakam vektörleri için kullanışlı değil. Rakam vektörleri için ayrı bir sistem gerek. Peki bu vektörü nasıl ifade edebiliriz?

15.2 Ortalama, ortanca ve dağılım

İlk seçeneğimiz aritmetik ortalama hesaplamak:

mean(iris$Sepal.Length)

[1] 5.843333

İkinci seçeneğimiz ortanca değeri hesaplamak:

median(iris$Sepal.Length)

[1] 5.8

Ortanca ve ortalama iki farklı istatistik aslında. Aritmetik ortalama, örneklem boyutuna bağlıdır. Bir $x$ vektörünün aritmetik ortalaması ($ $), aşağıdaki gibi hesaplanabilir:

\[ \overline{x} = \frac{\sum_{i=i}^{n} x_{i}}{n} \]

Ortanca değer ise bir vektörü küçükten büyüğe doğru sıraladığınzda, en ortada elde edilen değerdir. Elemanların yarısı bu değerin altında, diğer yarısı ise bu değerin üzerinde bulunur.

Peki verimizin sınırları ne? Bunun için tekrar summary fonksiyonuna bakalım:

summary(iris$Sepal.Length)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  4.300   5.100   5.800   5.843   6.400   7.900

Elde ettiğimiz ilk değer, en küçük elemanı gösteriyor. En sonraki değer ise en büyük elemanı. Aynı zamanda bu şekilde de hesaplayabiliriz:

min(iris$Sepal.Length)

[1] 4.3

max(iris$Sepal.Length)

[1] 7.9

Aynı zamanda ortanca (median) ve aritmetik ortalama (mean) değerleri de hesaplanmış. Peki 1st Qu. ve 3rd Qu. nedir?

Bu değerler çeyreklik olarak isimlendirilir. Elimizdeki veriyi, her bir parça toplam rakamların %25’ini içerecek şekilde 4 parçaya böldüğümüzde, elde ettiğimiz her bölge çeyreklik olarak isimlendirilir. Bu değerleri daha iyi anlamak için quantile fonksiyonunu kullanalım:

quantile(iris$Sepal.Length)

  0%  25%  50%  75% 100% 
 4.3  5.1  5.8  6.4  7.9

0% aslında en küçük değeri, 100% ise en büyük değeri gösteriyor. 4.3’ e kadar ilk çeyreklik kısım, 5.1’ye kadar ikinci çeyreklik, 6.4’e kadar üçüncü çeyreklik ve 7.9’ya kadar ise son çeyreklik kısım bulunur. İsterseniz rakamları sıralamamızı sağlayan sort fonksiyonu ile daha rahat görebiliriz:

sort(iris$Sepal.Length)

  [1] 4.3 4.4 4.4 4.4 4.5 4.6 4.6 4.6 4.6 4.7 4.7 4.8 4.8 4.8 4.8 4.8 4.9 4.9
 [19] 4.9 4.9 4.9 4.9 5.0 5.0 5.0 5.0 5.0 5.0 5.0 5.0 5.0 5.0 5.1 5.1 5.1 5.1
 [37] 5.1 5.1 5.1 5.1 5.1 5.2 5.2 5.2 5.2 5.3 5.4 5.4 5.4 5.4 5.4 5.4 5.5 5.5
 [55] 5.5 5.5 5.5 5.5 5.5 5.6 5.6 5.6 5.6 5.6 5.6 5.7 5.7 5.7 5.7 5.7 5.7 5.7
 [73] 5.7 5.8 5.8 5.8 5.8 5.8 5.8 5.8 5.9 5.9 5.9 6.0 6.0 6.0 6.0 6.0 6.0 6.1
 [91] 6.1 6.1 6.1 6.1 6.1 6.2 6.2 6.2 6.2 6.3 6.3 6.3 6.3 6.3 6.3 6.3 6.3 6.3
[109] 6.4 6.4 6.4 6.4 6.4 6.4 6.4 6.5 6.5 6.5 6.5 6.5 6.6 6.6 6.7 6.7 6.7 6.7
[127] 6.7 6.7 6.7 6.7 6.8 6.8 6.8 6.9 6.9 6.9 6.9 7.0 7.1 7.2 7.2 7.2 7.3 7.4
[145] 7.6 7.7 7.7 7.7 7.7 7.9

Tam olmasa da yaklaşık olarak eşit sayıda gruplar olduğu görülmekte.

Son olarak cut isimli fonksiyonlar benzer bir çalışma yapabiliriz. Bu fonksiyon, elimizdeki bir rakam vektörünü, istediğimiz aralıklarla bölmemizi sağlar. Mesela Sepal.Length vektörünü, en küçük elemanı koruyacak şekilde 4 parçaya ayıralım:

cut(iris$Sepal.Length, 4, include.lowest = TRUE)

  [1] [4.3,5.2] [4.3,5.2] [4.3,5.2] [4.3,5.2] [4.3,5.2] (5.2,6.1] [4.3,5.2]
  [8] [4.3,5.2] [4.3,5.2] [4.3,5.2] (5.2,6.1] [4.3,5.2] [4.3,5.2] [4.3,5.2]
 [15] (5.2,6.1] (5.2,6.1] (5.2,6.1] [4.3,5.2] (5.2,6.1] [4.3,5.2] (5.2,6.1]
 [22] [4.3,5.2] [4.3,5.2] [4.3,5.2] [4.3,5.2] [4.3,5.2] [4.3,5.2] [4.3,5.2]
 [29] [4.3,5.2] [4.3,5.2] [4.3,5.2] (5.2,6.1] [4.3,5.2] (5.2,6.1] [4.3,5.2]
 [36] [4.3,5.2] (5.2,6.1] [4.3,5.2] [4.3,5.2] [4.3,5.2] [4.3,5.2] [4.3,5.2]
 [43] [4.3,5.2] [4.3,5.2] [4.3,5.2] [4.3,5.2] [4.3,5.2] [4.3,5.2] (5.2,6.1]
 [50] [4.3,5.2] (6.1,7]   (6.1,7]   (6.1,7]   (5.2,6.1] (6.1,7]   (5.2,6.1]
 [57] (6.1,7]   [4.3,5.2] (6.1,7]   [4.3,5.2] [4.3,5.2] (5.2,6.1] (5.2,6.1]
 [64] (5.2,6.1] (5.2,6.1] (6.1,7]   (5.2,6.1] (5.2,6.1] (6.1,7]   (5.2,6.1]
 [71] (5.2,6.1] (5.2,6.1] (6.1,7]   (5.2,6.1] (6.1,7]   (6.1,7]   (6.1,7]  
 [78] (6.1,7]   (5.2,6.1] (5.2,6.1] (5.2,6.1] (5.2,6.1] (5.2,6.1] (5.2,6.1]
 [85] (5.2,6.1] (5.2,6.1] (6.1,7]   (6.1,7]   (5.2,6.1] (5.2,6.1] (5.2,6.1]
 [92] (5.2,6.1] (5.2,6.1] [4.3,5.2] (5.2,6.1] (5.2,6.1] (5.2,6.1] (6.1,7]  
 [99] [4.3,5.2] (5.2,6.1] (6.1,7]   (5.2,6.1] (7,7.9]   (6.1,7]   (6.1,7]  
[106] (7,7.9]   [4.3,5.2] (7,7.9]   (6.1,7]   (7,7.9]   (6.1,7]   (6.1,7]  
[113] (6.1,7]   (5.2,6.1] (5.2,6.1] (6.1,7]   (6.1,7]   (7,7.9]   (7,7.9]  
[120] (5.2,6.1] (6.1,7]   (5.2,6.1] (7,7.9]   (6.1,7]   (6.1,7]   (7,7.9]  
[127] (6.1,7]   (5.2,6.1] (6.1,7]   (7,7.9]   (7,7.9]   (7,7.9]   (6.1,7]  
[134] (6.1,7]   (5.2,6.1] (7,7.9]   (6.1,7]   (6.1,7]   (5.2,6.1] (6.1,7]  
[141] (6.1,7]   (6.1,7]   (5.2,6.1] (6.1,7]   (6.1,7]   (6.1,7]   (6.1,7]  
[148] (6.1,7]   (6.1,7]   (5.2,6.1]
Levels: [4.3,5.2] (5.2,6.1] (6.1,7] (7,7.9]

Bu işlem, vektörü 4 parçaya böldü ve her elemanı bir gruba dahil eden bir faktör vektörü geri döndürdü. Şimdi ise quantile fonksiyonunun çıktısını, kesim noktaları olarak tanımlayalım:

cut(iris$Sepal.Length, quantile(iris$Sepal.Length), include.lowest = TRUE)

  [1] [4.3,5.1] [4.3,5.1] [4.3,5.1] [4.3,5.1] [4.3,5.1] (5.1,5.8] [4.3,5.1]
  [8] [4.3,5.1] [4.3,5.1] [4.3,5.1] (5.1,5.8] [4.3,5.1] [4.3,5.1] [4.3,5.1]
 [15] (5.1,5.8] (5.1,5.8] (5.1,5.8] [4.3,5.1] (5.1,5.8] [4.3,5.1] (5.1,5.8]
 [22] [4.3,5.1] [4.3,5.1] [4.3,5.1] [4.3,5.1] [4.3,5.1] [4.3,5.1] (5.1,5.8]
 [29] (5.1,5.8] [4.3,5.1] [4.3,5.1] (5.1,5.8] (5.1,5.8] (5.1,5.8] [4.3,5.1]
 [36] [4.3,5.1] (5.1,5.8] [4.3,5.1] [4.3,5.1] [4.3,5.1] [4.3,5.1] [4.3,5.1]
 [43] [4.3,5.1] [4.3,5.1] [4.3,5.1] [4.3,5.1] [4.3,5.1] [4.3,5.1] (5.1,5.8]
 [50] [4.3,5.1] (6.4,7.9] (5.8,6.4] (6.4,7.9] (5.1,5.8] (6.4,7.9] (5.1,5.8]
 [57] (5.8,6.4] [4.3,5.1] (6.4,7.9] (5.1,5.8] [4.3,5.1] (5.8,6.4] (5.8,6.4]
 [64] (5.8,6.4] (5.1,5.8] (6.4,7.9] (5.1,5.8] (5.1,5.8] (5.8,6.4] (5.1,5.8]
 [71] (5.8,6.4] (5.8,6.4] (5.8,6.4] (5.8,6.4] (5.8,6.4] (6.4,7.9] (6.4,7.9]
 [78] (6.4,7.9] (5.8,6.4] (5.1,5.8] (5.1,5.8] (5.1,5.8] (5.1,5.8] (5.8,6.4]
 [85] (5.1,5.8] (5.8,6.4] (6.4,7.9] (5.8,6.4] (5.1,5.8] (5.1,5.8] (5.1,5.8]
 [92] (5.8,6.4] (5.1,5.8] [4.3,5.1] (5.1,5.8] (5.1,5.8] (5.1,5.8] (5.8,6.4]
 [99] [4.3,5.1] (5.1,5.8] (5.8,6.4] (5.1,5.8] (6.4,7.9] (5.8,6.4] (6.4,7.9]
[106] (6.4,7.9] [4.3,5.1] (6.4,7.9] (6.4,7.9] (6.4,7.9] (6.4,7.9] (5.8,6.4]
[113] (6.4,7.9] (5.1,5.8] (5.1,5.8] (5.8,6.4] (6.4,7.9] (6.4,7.9] (6.4,7.9]
[120] (5.8,6.4] (6.4,7.9] (5.1,5.8] (6.4,7.9] (5.8,6.4] (6.4,7.9] (6.4,7.9]
[127] (5.8,6.4] (5.8,6.4] (5.8,6.4] (6.4,7.9] (6.4,7.9] (6.4,7.9] (5.8,6.4]
[134] (5.8,6.4] (5.8,6.4] (6.4,7.9] (5.8,6.4] (5.8,6.4] (5.8,6.4] (6.4,7.9]
[141] (6.4,7.9] (6.4,7.9] (5.1,5.8] (6.4,7.9] (6.4,7.9] (6.4,7.9] (5.8,6.4]
[148] (6.4,7.9] (5.8,6.4] (5.8,6.4]
Levels: [4.3,5.1] (5.1,5.8] (5.8,6.4] (6.4,7.9]

Son olarak elde ettiğimiz faktör vektörünün frekans tablosunu elde edelim:

table(cut(iris$Sepal.Length, quantile(iris$Sepal.Length), include.lowest = TRUE))


[4.3,5.1] (5.1,5.8] (5.8,6.4] (6.4,7.9] 
       41        39        35        35

Yaklaşık olarak eşit gruplar elde ettik. Sonuç olarak verimizin dağılımı bu şekilde:

15.3 Hatta grafiğini yapalım!

R bize aynı zamanda bu dağılımı görselleştirme imkanı da sunuyor. Mesela kutu grafikleri (boxplot) elimizdeki verinin dağılımını gösteren yegane görselleştirme metodudur. Burada boxplot fonksiyonu ile birlikte bir rakam vektörü kullanmamız gerektiğine dikkat edin lütfen. Yani sadece sürekli (continious) veri tipleriyle işlem yapabiliriz. Faktör gibi kategori (disecrete) veri tipleri tek başlarına kullanılamaz.

Burada kullandığımız outline opsiyonu, outlier değerlerin gösterilmemesi gerektiğini belirtmektedir.

boxplot(iris$Sepal.Length, outline = FALSE)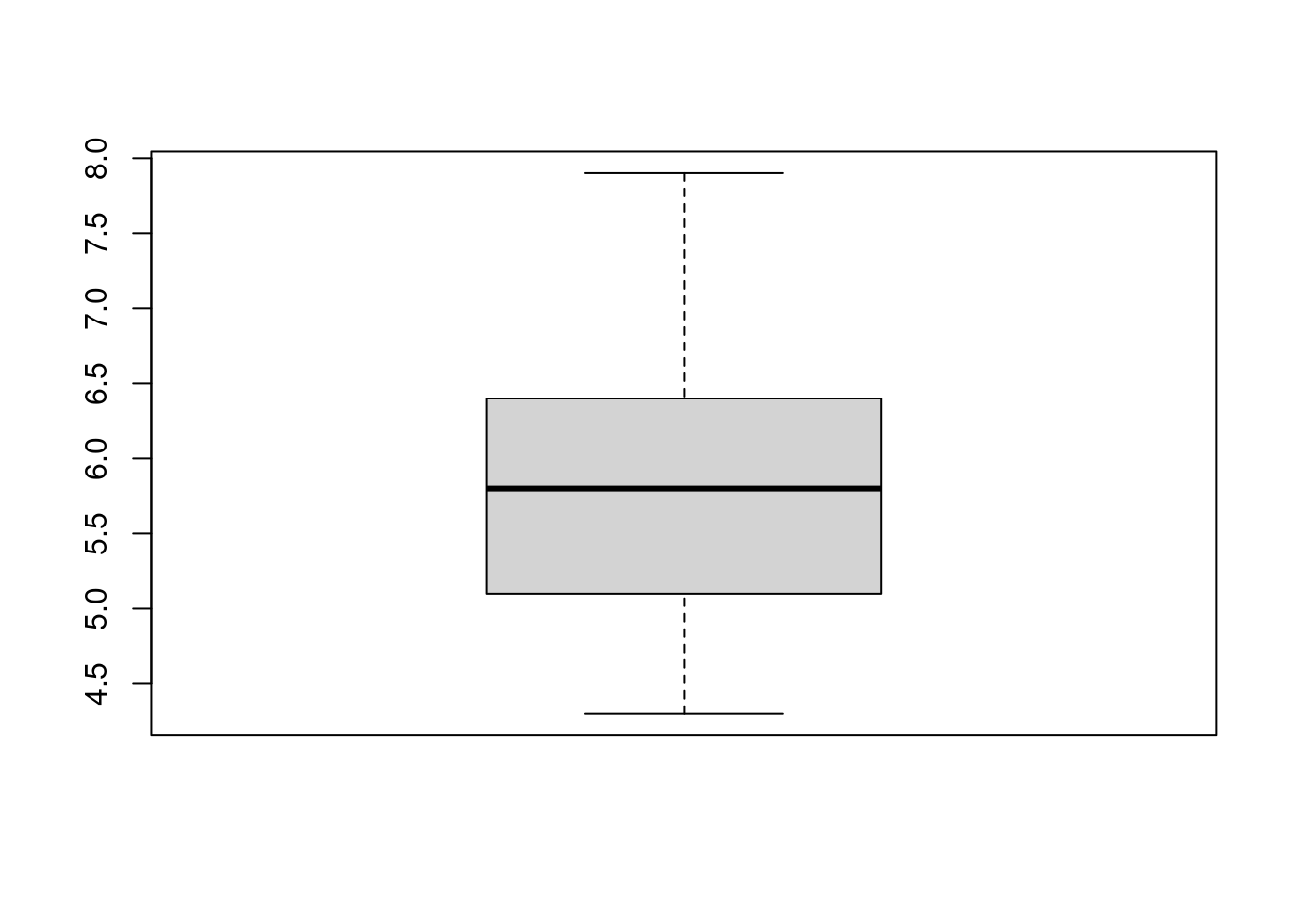

Kutu grafikleri, sürekli veri tiplerinin dağılımını görselleştirir; - Ortadaki kalın çizgi bize ortanca değeri gösterir, - En aşağıdaki çizgi ise minimum değeri, - Kesikli çizgi birinci çeyreklik kısmı, - Kutu içerisinde ikinci ve üçüncü çeyreklik kısımlar ortanca değer ile ayrılır, - En üstteki değerle kutunun arasındaki kesikli çizgi ise dördüncü çeyrekliği gösterir.

summary(iris$Sepal.Length)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  4.300   5.100   5.800   5.843   6.400   7.900

En küçük değer 4.3, en büyük ise 7.9 oluyor. İstersek petal uzunlukları için de aynısını gerçekleştirebiliriz.

boxplot(iris$Petal.Length)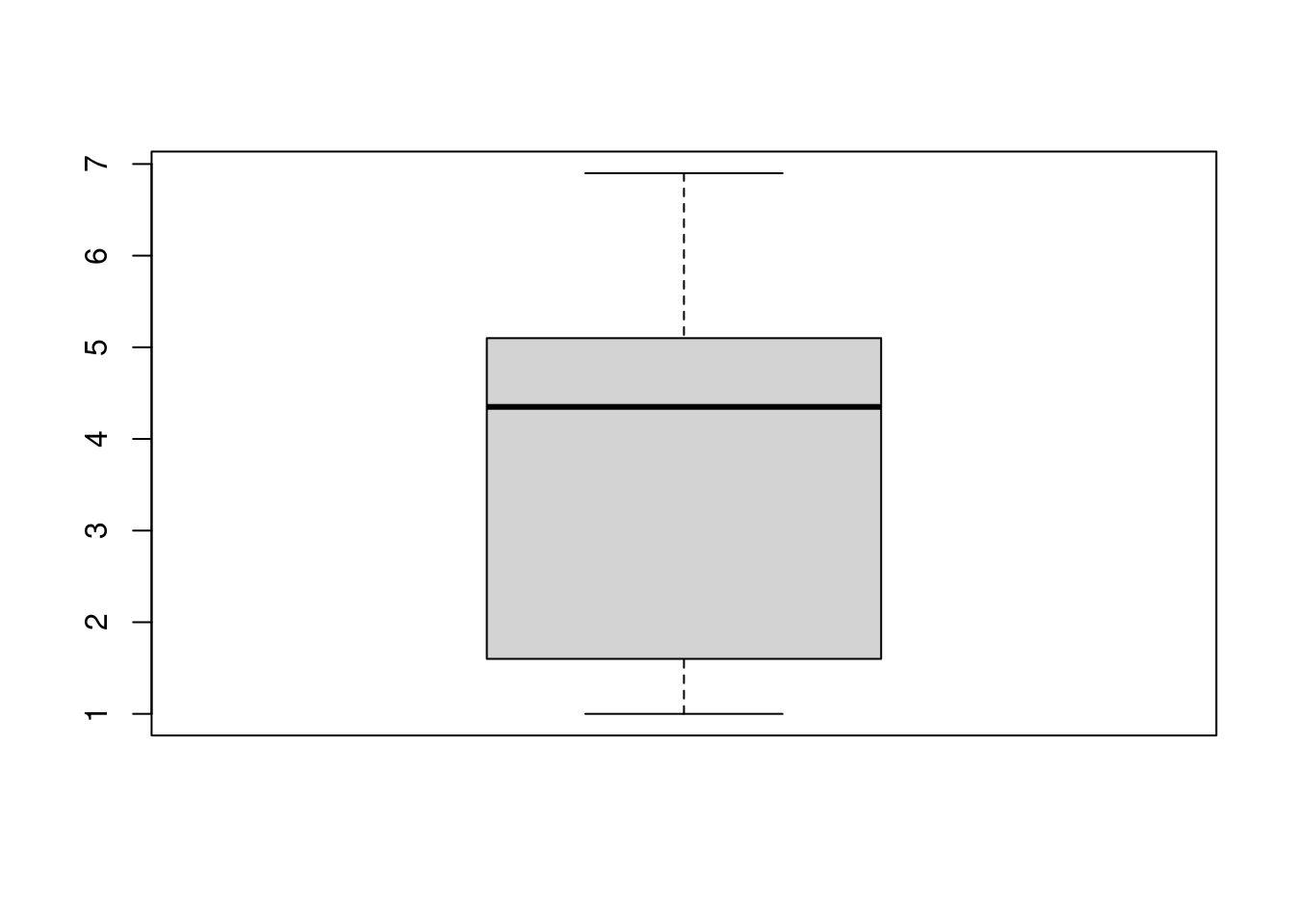

15.3.1 Bağlantıları kurmak: Hikaye anlatımı

Peki Sepal Uzunluğunun Türler ile olan ilişkisi nasıldır?

boxplot(iris$Sepal.Length~iris$Species)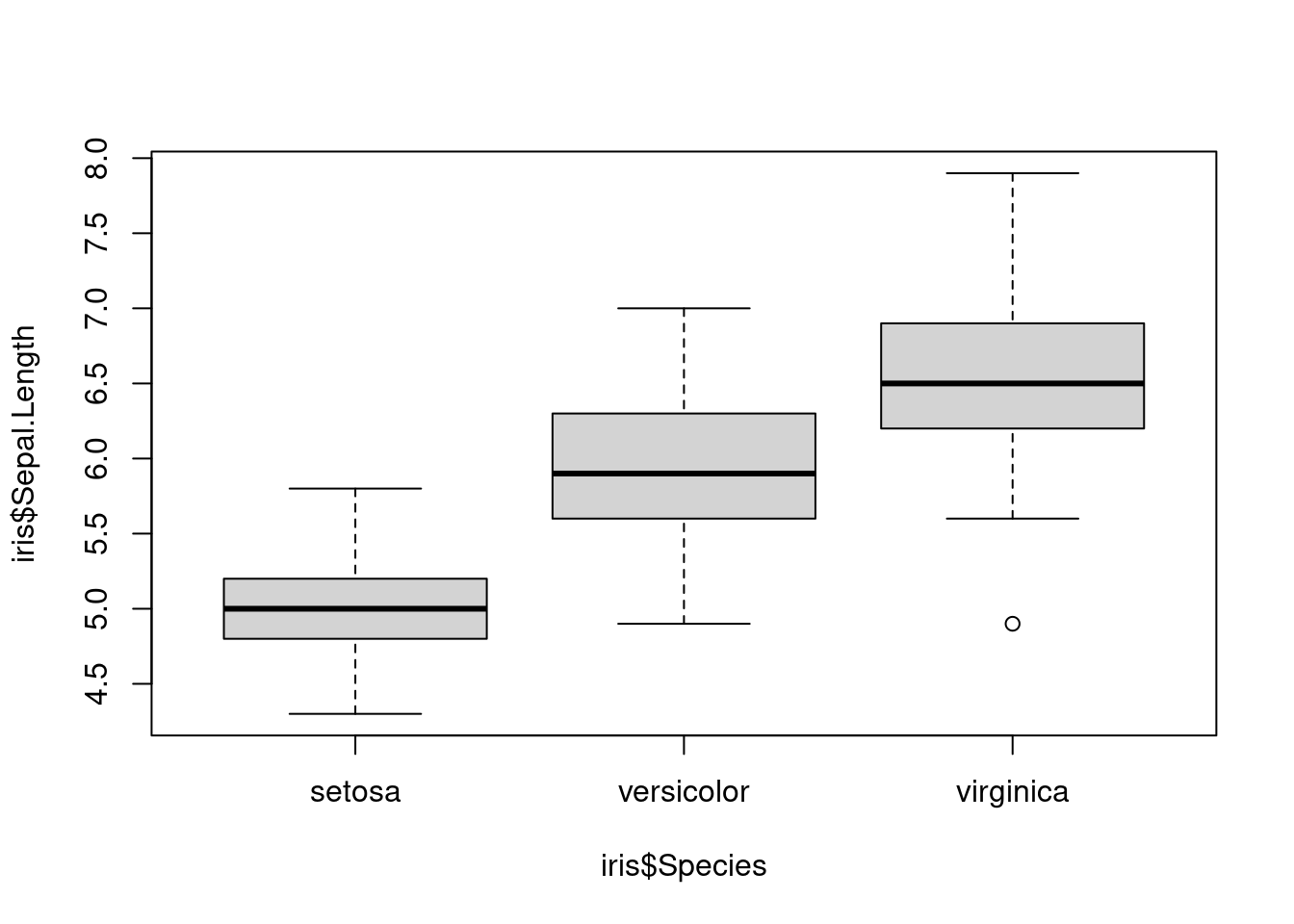

Burada ~ işareti (sağ alt tuşu + ü), soldaki değeri, sağdaki değere göre ifade et şeklinde özetlenebilir. Aslında bir değişkeni, başka bir değişken kullanarak modelliyoruz. Bu konuya ilerleyen derslerde geleceğiz.

Soru

Acaba bu grafikte ne dikkatinizi çekti? Derse 5 dakika ara veriniz ve sohbet kısmından yorumlarınızı yazınız.

15.4 `ggplot2`: İleri seviye görselleştirme

Buraya kadar normal R grafiklerini gördük. Ancak R üzerinde başka görselleştirme kütüphaneleri de mevcuttur. Bunlardan bir tanesi de ggplot2.

Bu kütüphaneyi kullanmak için öncelikle, R içerisine yükleme yapmalyız:

install.packages("ggplot2")

Şimdi yüklediğimiz kütüphaneyi, R içerisine aktaralım:

library(ggplot2)

Kutu grafiğini yapalım:

ggplot(data = iris, aes(x = Sepal.Length, y = Species)) + geom_boxplot()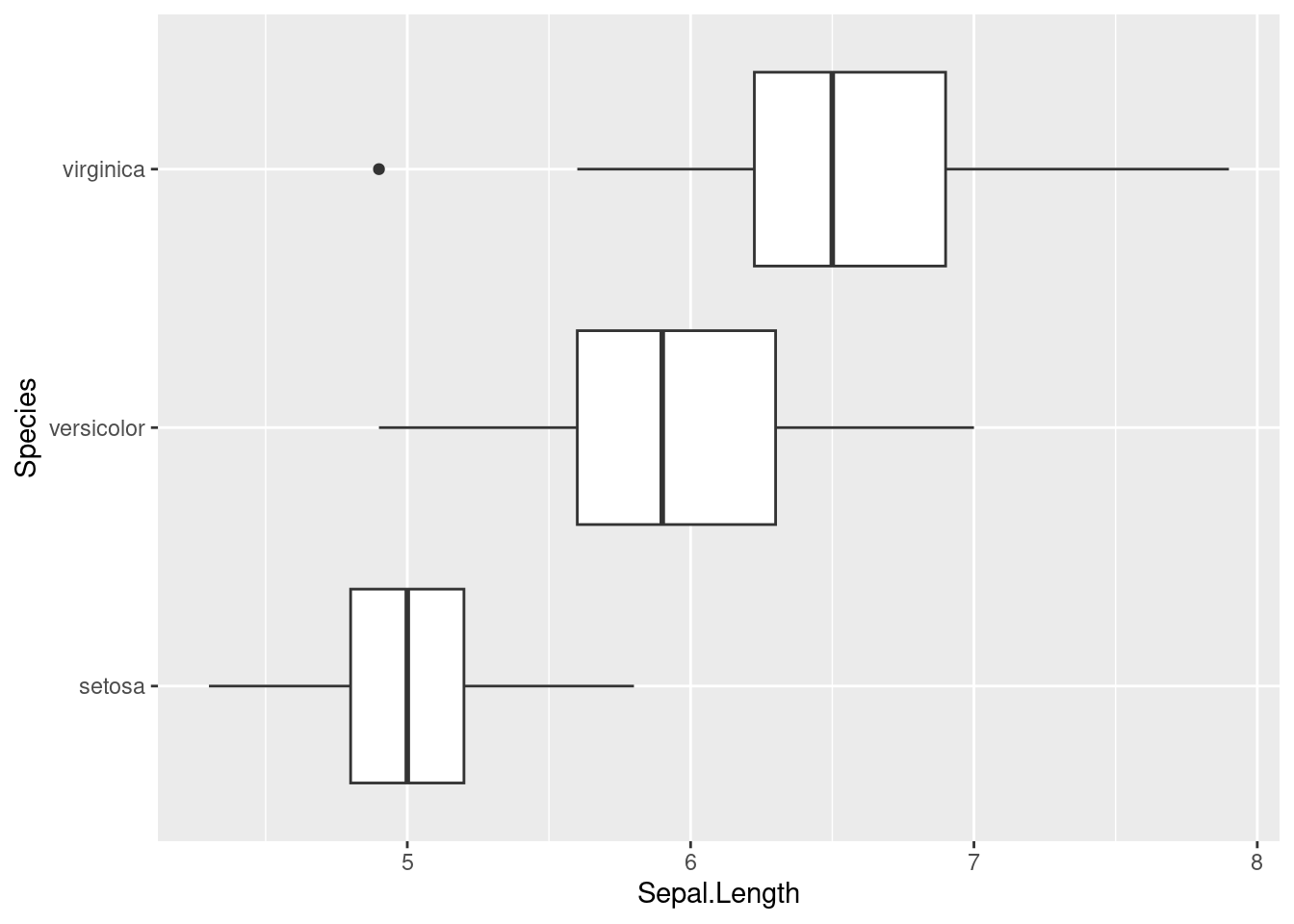

Haftaya daha ayrıntılı işleyeceğiz!

15.1 Tanımlayıcı istatistikler

15.1.1 Frekans tabloları

15.2 Ortalama, ortanca ve dağılım

15.3 Hatta grafiğini yapalım!

15.3.1 Bağlantıları kurmak: Hikaye anlatımı

15.4 ggplot2: İleri seviye görselleştirme

15.4 `ggplot2`: İleri seviye görselleştirme