18 T-Test

Bu döküman kapsamında R üzerinde t-test ile ile ilgili bilgiler verilecektir.

18.1 t.test()

Tanım olarak t-testi, iki grubun ortalamaları arasında anlamlı bir fark olup olmadığını test etmek için kullanılabilir.

Bunu göstermek için iki farklı dağlım simüle edelim.

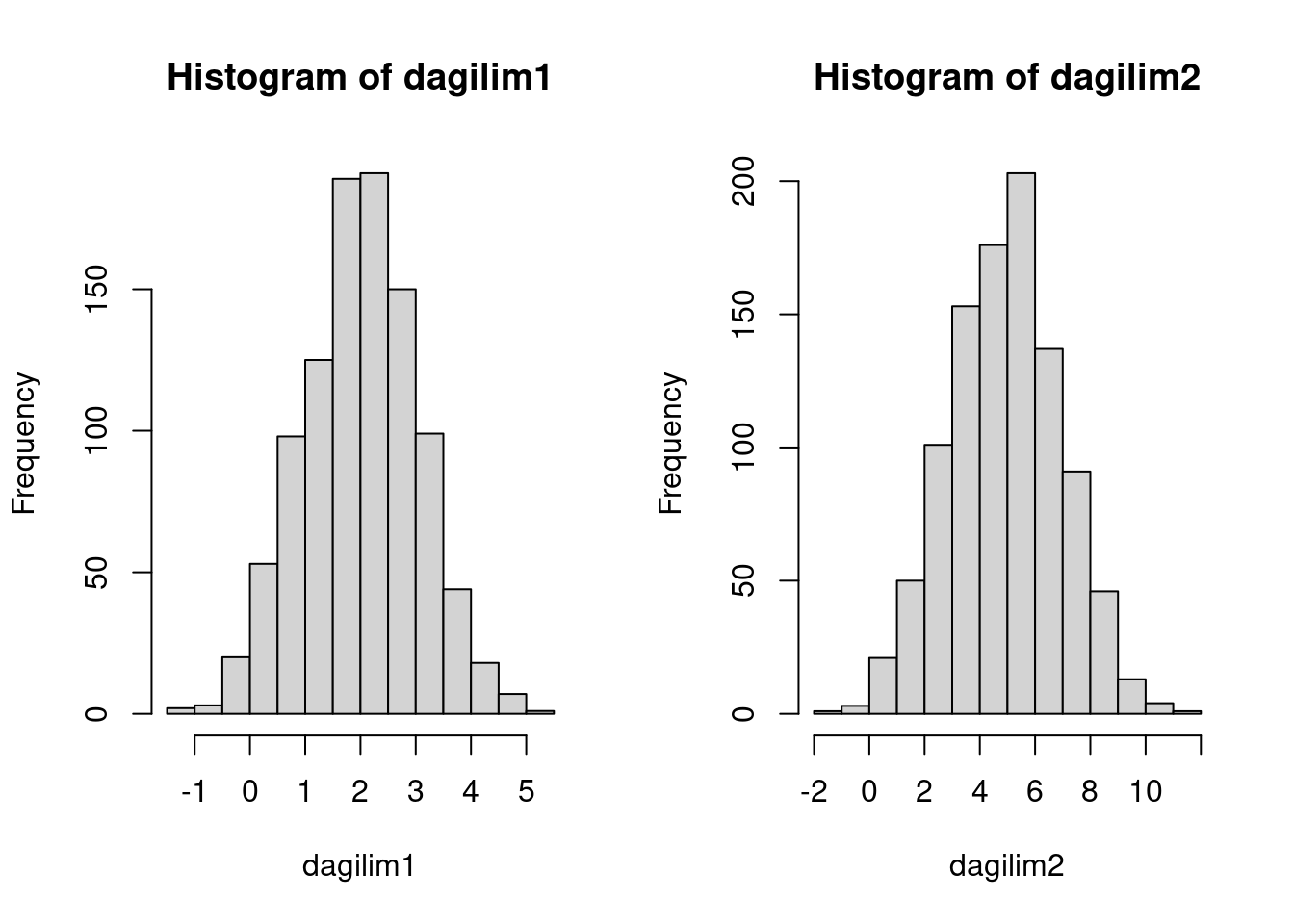
dağılım1, örnek sayısı = 1000, ortalama = 2, standart sapma = 1
dağılım2, örnek sayısı = 1000, ortalama = 5, standart sapma = 2

dagilim1 <- rnorm(n = 1000, mean = 2, sd = 1)
dagilim2 <- rnorm(n = 1000, mean = 5, sd = 2)

Histogramlar ile bu dağılımları inceleyelim:

par(mfrow=c(1,2))
hist(dagilim1)
hist(dagilim2)

İstersek yoğunluk grafiğiyle de bunu görselleştirebiliriz. Burada iki dağılımı alıp, bir veri çerçevesinin içersine yerleştirdik ve dagilim1 ve dagilim2 olarak iki farklı faktör verisi oluşturduk:

sim <- data.frame(
  dagilim = c(dagilim1, dagilim2), 
  seviye = c(
    rep("dagilim1", 1000), 
    rep("dagilim2", 1000)
    )
  )

library(ggplot2)

ggplot(data = sim, aes(x=dagilim)) + geom_density(aes(fill = seviye), alpha = 0.9)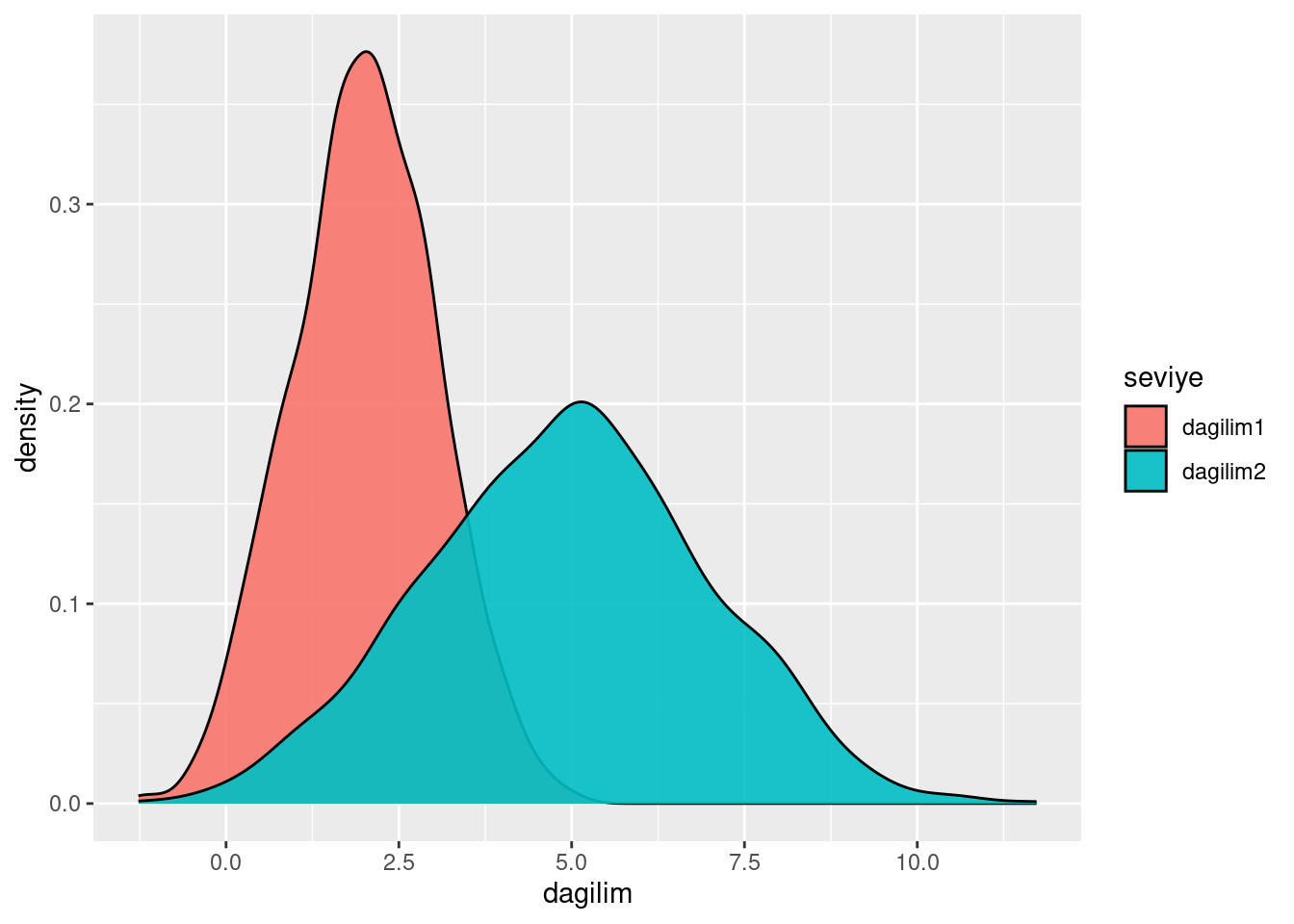

Dikkat ederseniz bu iki dağılımın ortalamarı birbirlerinden farklı. Peki bu fark anlamlı mı? Bunu tespit etmek için t.test kullanabiliriz:

test <- t.test(x = dagilim1, y = dagilim2)

test


    Welch Two Sample t-test

data:  dagilim1 and dagilim2
t = -40.732, df = 1495.1, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -3.054893 -2.774177
sample estimates:
mean of x mean of y 
 2.009660  4.924195

Burada dikkat etmemiz gereken iki nokta var:

mean of x, mean of y satırı
p-value

P value bizim için önemli bir değer. T testi sonunda elde ettiğimiz p-değerini şu şekilde geri döndürebiliriz:

test$p.value

[1] 1.22019e-244

Dikkat ederseniz bu değer çok düşük. Bu sonuç aslında bu iki dağılımın ortalamalarının birbirlerinden farklı olduğunu gösteriyor bize.

18.2 Hipotez testi

Bu kısım biraz kafa karıştırıcı. Eğer ilk dersleri hatırlarsanız, bilimde bir şeyi doğrudan kanıtlayamadığımızı hatırlarsınız. Bu nedenle bir hipotezi doğrudan kanıtlama imkanımız yoktur. Bir hipotezi, ancak onun karşıtını reddederek kabul edebiliriz.

Nasıl mı? Bir önceki örnekte iki dağılımın birbirinden farklı olduğu hipotezini ortaya atmıştık. Bu mantığa göre, bu hipotezi test etmenin yolu, bu hipotezin zıddını test etmekten geçer.

Yani aslında ortaya iki tane hipotez atıyoruz:

H0 (sıfır hipotezi): Bu iki dağılımın ortamaları birbirine eşittir.
HA (alternatif hipotez): Bu iki dağılımın ortalamarı birbirinden farklıdır.

Yapmaya çalıştığımız ise doğrudan sıfır hipotezini reddetmeye çalışmak. Bu sayede alternatif hipotezi kabul edebiliriz.

Testimiz sonucunda bir p-değeri elde etmiştik hatırlarsınız. Bu p-değeri işte sıfır hipotezinin oluşma olasılığını ifade etmekte. Bizim elde ettiğimiz p-değeri neydi?

test$p.value

[1] 1.22019e-244

Bu değer çok çok çok düşük bir değer. Yani bu iki dağılımın ortalamalarının aynı olması çok düşük bir olasılık. Bu olasılığın anlamlı olup olmadığını öğrenmek için ise belirli \(alpha\) değerleri kullanılır:

0.001 (binde 1 hata olasılığı)
0.01 (%1 hata olasılığı)
0.05 (%5 hata olasığı)

Örnek vermek gerekirse, 0.0001 \(alpha\) değeri altında elde ettiğimiz sonuç anlamlı mı?

test$p.value < 0.001

[1] TRUE

Şimdi tekrar örneğimize geri dönelim:

test


    Welch Two Sample t-test

data:  dagilim1 and dagilim2
t = -40.732, df = 1495.1, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -3.054893 -2.774177
sample estimates:
mean of x mean of y 
 2.009660  4.924195

Şu satıra bakalım:

alternative hypothesis: true difference in means is not equal to 0

Bunun anlamı aslında şu: 0.0001 hata olasılığı durumunda, bu iki dağılımın ortalamaları anlamlı bir şekilde farklı! Yani sıfır hipotezini reddedip, alternatif hipotezi kabul ediyoruz!

18.3 İkinci bir örnek

Şimdi ise, birbirine çok benzer iki dağılım simüle edelim:

dağılım1, örnek sayısı = 1000, ortalama = 2, standart sapma = 1
dağılım2, örnek sayısı = 1000, ortalama = 2, standart sapma = 2

dagilim1 <- rnorm(n = 1000, mean = 2, sd = 1)
dagilim2 <- rnorm(n = 1000, mean = 2, sd = 1)

sim <- data.frame(
  dagilim = c(dagilim1, dagilim2), 
  seviye = c(
    rep("dagilim1", 1000), 
    rep("dagilim2", 1000)
    )
  )

library(ggplot2)

ggplot(data = sim, aes(x=dagilim)) + geom_density(aes(fill = seviye), alpha = 0.9)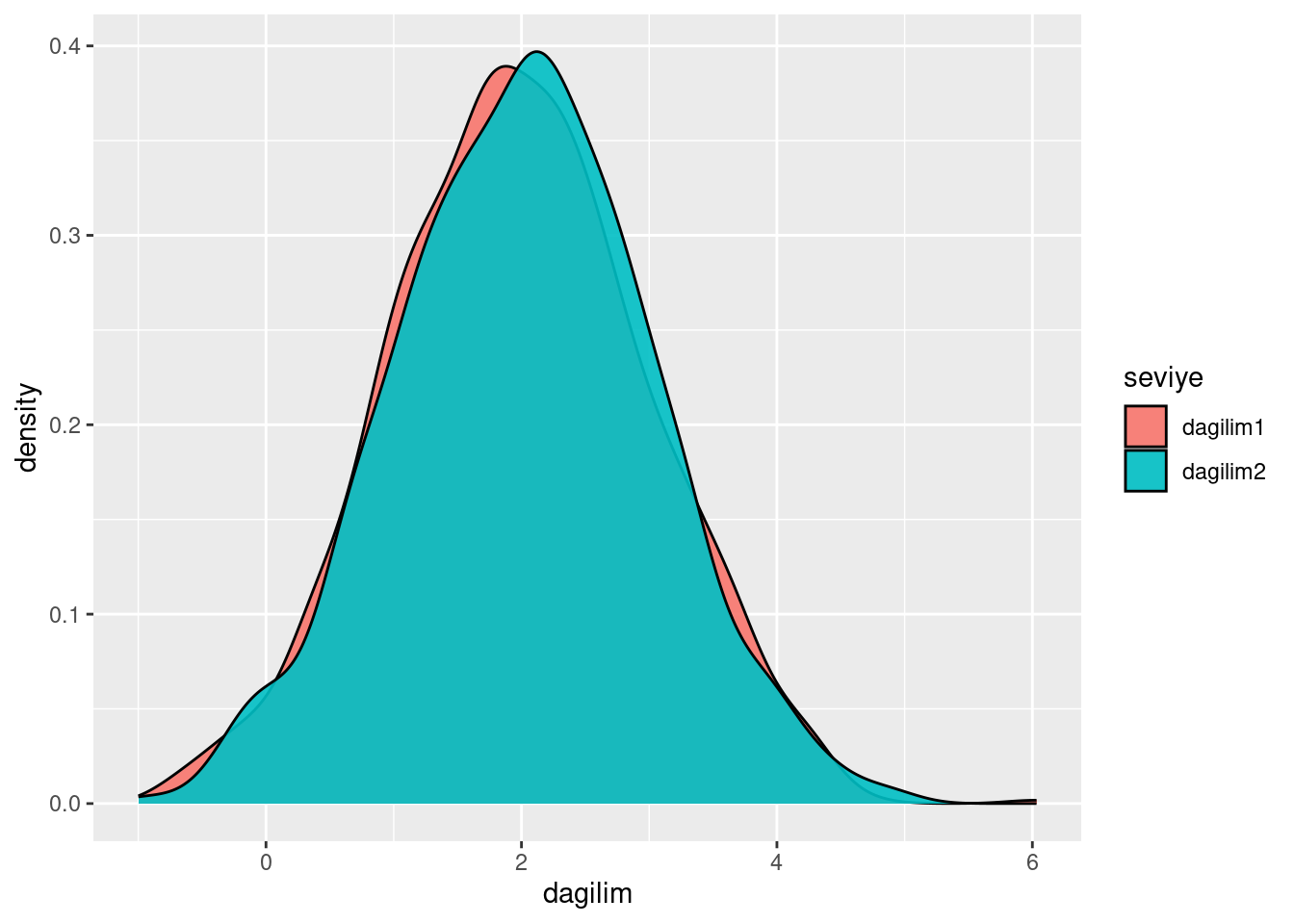

Dikkat ederseniz bu dağılımların ortalamaları üst üste bindi. Peki t-testi uygularsak nasıl bir sonuç elde edeceğiz?

test <- t.test(x = dagilim1, y = dagilim2)

test


    Welch Two Sample t-test

data:  dagilim1 and dagilim2
t = -0.8776, df = 1997.6, p-value = 0.3803
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -0.12678242  0.04839289
sample estimates:
mean of x mean of y 
 1.976379  2.015574

Bu sonuçta bakmamız gereken şey aslında şu: Bu iki dağılımın ortalamaları çok az da olsa birbirlerinden farklı. Peki bu farklılık anlamlı mı?

test$p.value< 0.001

[1] FALSE

Eğer 0.001 \(alpha\) değerini seçtiğimizde bu iki popülasyonun ortamalarının aynı olma ihtimalinin çok yüksek olduğunu görüyoruz. Bu nedenle sıfır hipotezini reddedmiyoruz.

18.4 Iris veri seti ile çalışma

Şimdi ise iris veri seti ile çalışalım.

Petal uzunluklarına bakabilir miyiz yine?

ggplot(data = iris, aes(x = Petal.Length)) + geom_density(aes(fill = Species), alpha = 0.7)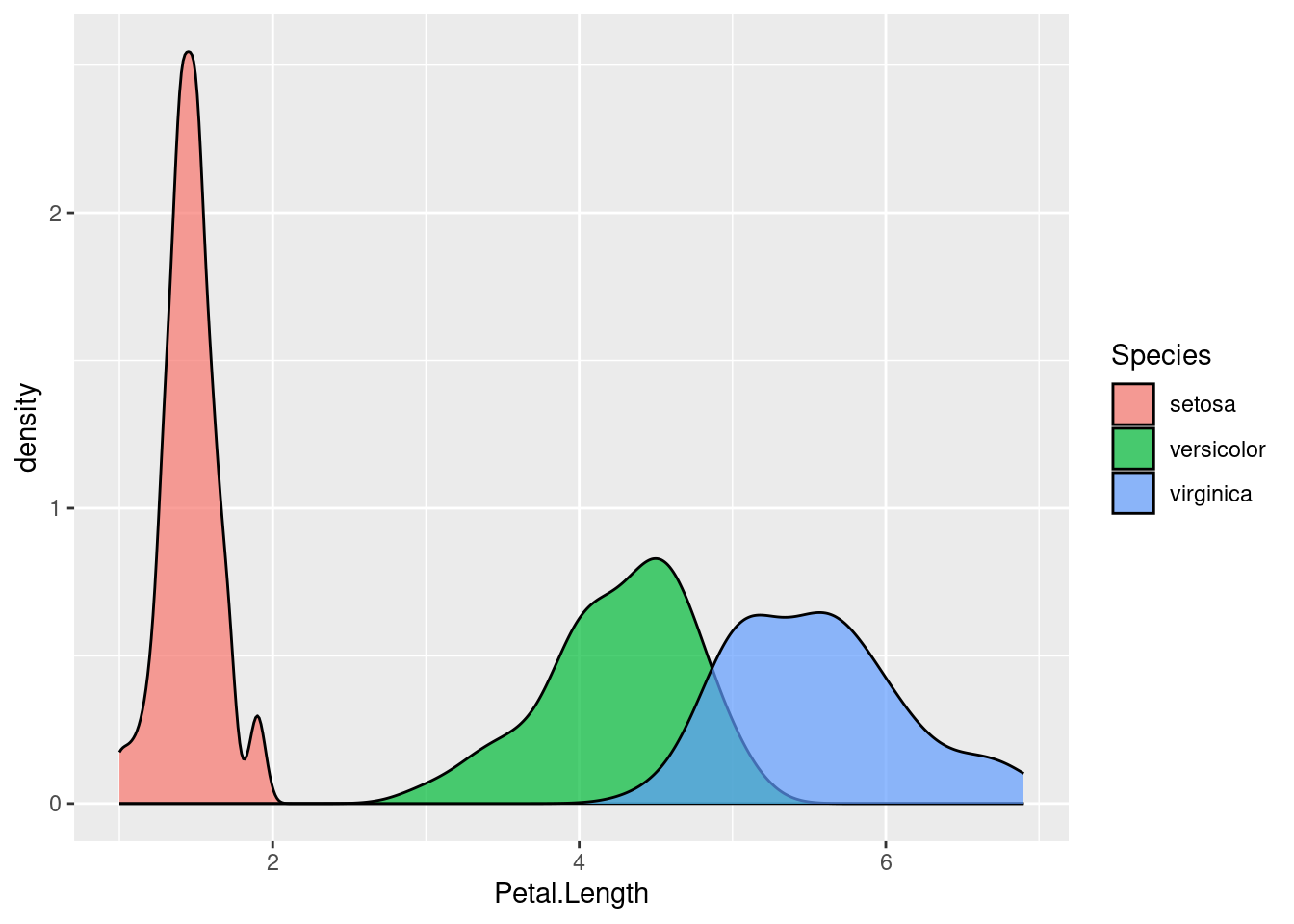

Acaba, versicolor ve virginica türlerinin petal uzunlukları birbirlerinden anlamlı olarak farklı mı (\(alpha\) değerini 0.05 alınız)?

Öncelikle sadece versicolor ve virginica türlerine ait petal uzunluklarının olduğu iki farklı vektör oluşturmalıyız:

versicolor_petal_length  <- iris$Petal.Length[iris$Species == "versicolor"]
virginica_petal_length  <- iris$Petal.Length[iris$Species == "virginica"]

Şimdi t testini uygulayalım:

test <- t.test(x = versicolor_petal_length, y = virginica_petal_length)

Sonuçları inceleyelim:

test


    Welch Two Sample t-test

data:  versicolor_petal_length and virginica_petal_length
t = -12.604, df = 95.57, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -1.49549 -1.08851
sample estimates:
mean of x mean of y 
    4.260     5.552

Peki sonuç anlamlı mı?

test$p.value < 0.05

[1] TRUE

Evet, versicolor ve virginica türlerinin petal uzunlukları birbirlerinden anlamlı olarak farklı!